Advertisements
Advertisements
प्रश्न
Find the area of minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 600 .
उत्तर
Area of the minor segment of the circle = \[\sqrt{2}\]\[\frac{\theta}{360} \times \pi r^2 - r^2 \sin\frac{\theta}{2}\cos\frac{\theta}{2}\]
\[= \frac{60}{360} \times \pi \left( 14 \right)^2 - \left( 14 \right)^2 \sin\frac{60}{2}\cos\frac{60}{2}\]
\[ = \left( 14 \right)^2 \left[ \frac{1}{6}\pi - \frac{1}{2} \times \frac{\sqrt{3}}{2} \right]\]
\[ = \left( \frac{308}{3} - 49\sqrt{3} \right) {cm}^2\]
APPEARS IN
संबंधित प्रश्न
A rectangular plot measure 125 m by 78 m. It has gravel path 3 m wide all around on the outside. Find the area of the path and the cost of gravelling it at` ₹ 75 per m^2`
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
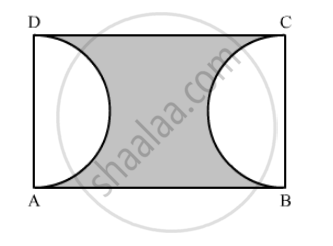
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
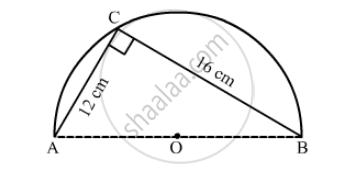
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
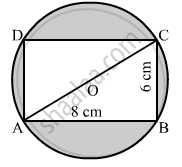
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
Find the area enclosed between two concentric circles of radii 6.3cm and 8.4cm. A third concentric circle is drawn outside the 8.4cm circle. So that the area enclosed between it and the 8.4cm circle is the same as that between the two inner circles. Find the radii of the third circle correct to two decimal places.
Find the length of the rope by which a bull must be tethered in order that it may be able to graze an area of 2464 m2
