Advertisements
Advertisements
प्रश्न
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
उत्तर
Given that, a triangular field with the three corners of the field a cow, a buffalo and a horse are tied separately with ropes.
So, each animal grazed the field in each corner of triangular field as a sectorial form.
Given, radius of each sector (r) = 7 m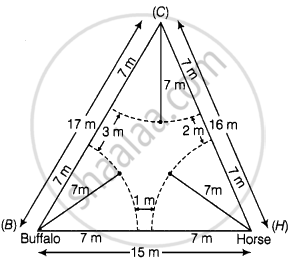
Now, area of sector with ∠C
= `(∠"C")/360^circ xx pi"r"^2`
= `(∠"C")/360^circ xx pi xx (7)^2"m"^2`
Area of the sector with ∠B
= `(∠"B")/360^circ xx pi"r"^2`
= `(∠"B")/360^circ xx pi xx (7)^2"m"^2`
And area of the sector with ∠H
= `(∠"H")/360^circ xx pi"r"^2`
= `(∠"H")/360^circ xx pi xx (7)^2"m"^2`
Therefore, sum of the area (in cm2) of the three sectors
= `(∠"C")/360^circ xx pi xx (7)^2 + (∠"B")/360^circ xx pi xx (7)^2 + (∠"H")/360^circ xx pi xx (7)^2`
= `((∠"C" + ∠"B" + ∠"H"))/360^circ xx pi xx 49`
= `180^circ/360^circ xx 22/7 xx 49`
= 11 × 7
= 77 cm2
Given that, sides of triangle are a = 15, b = 16 and c = 17
Now, semi-perimeter of triangle,
s = `("a" + "b" + "c")/2`
⇒ `(15 + 16 + 17)/2 = 48/2` = 24
∴ Area of triangular field
= `sqrt("s"("s" - "a")("s" - "b")("s" - "c"))` ...[By Heron's formula]
= `sqrt(24 * 9 * 8* 7)`
= `sqrt(64 * 9 * 21)`
= `8 xx 3sqrt(21)`
= `24sqrt(21) "m"^2`
So, area of the field which cannot be grazed by the three animals
= Area of triangular field – Area of each sectorial field
= `24sqrt(21) - 77 "m"^2`
Hence, the required area of the field which cannot be grazed by the three animals is `(24sqrt(21) - 77) "m"^2`.
संबंधित प्रश्न
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area. What area will be left ungrazed?
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
