Advertisements
Advertisements
рдкреНрд░рд╢реНрди
A plot is in the form of rectangle ABCD having semi-circle on BC. If AB = 60m and BC = 28m, find the area of plot.
рдЙрддреНрддрд░
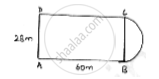
Given AB = 60m = DC [length]
BC = 28m = AD [breadth]
Radius of semicircle r =`1/2`× ЁЭР╡ЁЭР╢ = 14ЁЭСЪ
Area of semicircle r =`1/2`× ЁЭР╡ЁЭР╢ = 14ЁЭСЪ
Area of plot = (Area of rectangle ABCD) + (area of semicircle)
= (ЁЭСЩЁЭСТЁЭСЫЁЭСФЁЭСбтДО × ЁЭСПЁЭСЯЁЭСТЁЭСОЁЭССЁЭСбтДО) +`1/2 pir^2`
= `(60 × 28) + [1/2×22/7× 14 × 14]`
= 1680 + 308 = 1988ЁЭСЪ2
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
An arc of a circle is of length 5π cm and the sector it bounds has an area of 20 π cm2. Find the radius of the circle.
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Area of the circle
The radius of the wheel of a vehicle is 42 cm. How many revolutions will it complete in a 19.8-km-long journey?
The difference between the circumference and radius of a circle is 37 cm. The area of the circle is
The circumferences of two circles are in the ratio 3 : 4. The ratio of their areas is
Find the area enclosed between two concentric circles, if their radii are 6 cm and 13 cm respectively.
Find the area and perimeter of the following semi-circle :
Radius= 1.4 cm
The radius of a circle is 21 cm. Find the circumference (Take π = `3 1/7`).
Find the diameter of a circle whose circumference is equal to the sum of circumference of circles with radius 10 cm, 12 cm, and 18 cm.
A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/sec, calculate the number of complete revolutions the wheel makes in raising the bucket. (Take π =22/7)
