Advertisements
Advertisements
प्रश्न
The circumferences of two circles are in the ratio 3 : 4. The ratio of their areas is
उत्तर
Let the the radii of the two circles be r and R, the circumferences of the circles be c and C and the areas of the two circles be a and A.
Now,
`c/C = 3/4`
`=>(2pi"r")/(2pi"R") = 3/4`
`=> "r"/"R" = 3/4`
Now, the ratio between their areas is given by
`"a"/"A" = (pi"r"^2)/(pi"R"^2)`
`=("r"/"R")^2`
`=(3/4)^2`
`= 9/16`
Hence, the correct answer is option (c).
APPEARS IN
संबंधित प्रश्न
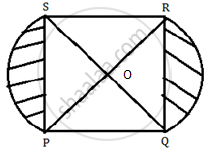
In the figure given below, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its
diagonals. Find the total area of the two flower beds (shaded parts).
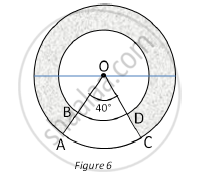
In Fig. 6, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. (use `pi = 22/7`)
A pendulum swings through an angle of 30º and describes an arc 8.8 cm in length. Find the length of the pendulum.
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days. (Take π = 22/7)
The side of a square is 10 cm. Find the area of the inscribed circle [π = 3.14]
Find the area and perimeter of the following sector :
Radius= 4.2 cm, angle at the centre is 60 °
Construct the circumcircle of the ABC when BC = 6 cm, B = 55° and C = 70°.
The cost of fencing a circular race course at the rate of ₹ 8 per metre is ₹ 2112. Find the diameter of the race course
The perimeter of a sector of radius 5.2 cm is 16.4 cm, the area of the sector is ____________.
The diameter of a wheel is 1.26 m. The distance traveled in 500 revolutions is ____________.
