Advertisements
Advertisements
प्रश्न
Find the area of the segment of a circle of radius 12 cm whose corresponding sector has a central angle of 60° (Use π = 3.14).
उत्तर
Radius of the circle = r = 12 cm
OA = OB = 12 cm
∠AOB = 60° .......(GIven)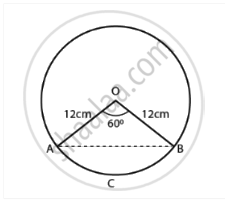
As triangle OAB is an isosceles triangle,
∠OAB = ∠OBA = θ .....(Let)
And sum of interior angles of a triangle is 180°,
θ + θ + 60° = 180°
2θ = 120°
θ = 60°
Therefore, the triangle AOB is an equilateral triangle.
AB = OA = OB = 12 cm
Area of the triangle AOB = `(sqrt(3)/4) xx a^2`.
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
(2) Area of any one of the sectors
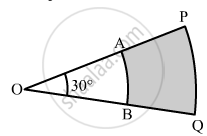
In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
