Advertisements
Advertisements
प्रश्न
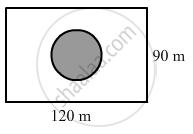
A park is in the form of a rectangle 120 m by 90 m. At the centre of the park there is a circular lawn as shown in the figure. The area of the park excluding the lawn is 2950 m2. Find the radius of the circular lawn.
उत्तर
Area of the rectangle = l × b
= 120 × 90
= 10800 sq. m
Area of the park excluding the lawn = 2950 m2
Area of the circular lawn = Area of the park -- Area of the park excluding the lawn
= 10800 - 2950
= 7850 m2
Area of the circular lawn =πr2
`=> 7850 = 22/7xx"r"^2`
`=> (7850) = 22/7xx"r"^2`
`=> "r"^2 = 2497.72`
⇒ r = 49.97
Or,
r ≈ 50 m
Thus, the radius of the circular lawn is 50 m.
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
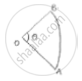
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
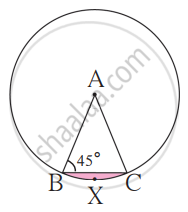
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.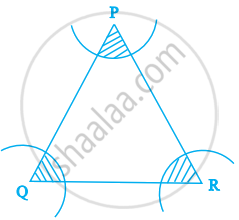
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
Find the perimeter of a quadrant of a circle of radius 14 cm.
