Advertisements
Advertisements
Question
Find the number of revolutions made by a circular wheel of area 1.54 m2 in rolling a distance of 176 m.
Solution
Let the number of revolutions made by a circular wheel be n and the radius of circular wheel be r.
Given that, area of circular wheel = 1.54 m2
⇒ πr2 = 1.54 ...[∵ Area of circular πr2]
⇒ r2 = `1.54/22 xx 7`
⇒ r2 = 0.49
∴ r = 0.7 m
So, the radius of the wheel is 0.7 m
Distance travelled by a circular wheel in one revolution = Circumference of circular wheel
= 2πr
= `2 xx 22/7 xx 0.7`
= `22/5`
= 4.4 m ...[∵ Circumference of a circle = 2πr]
Since, distance travelled by a circular wheel = 176 m
∴ Number of revolutions = `"Total distance"/"Distance in one revolution"`
= `176/4.4`
= 40
Hence, the required number of revolutions made by a circular wheel is 40.
APPEARS IN
RELATED QUESTIONS
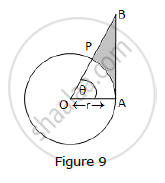
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
The area of rhombus is `480cm^2` , and one of its diagonal measures 48 cm. Find
(i) the length of the other diagonal,
(ii) the length of each of the sides
(iii) its perimeter
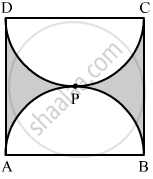
Find the perimeter of the shaded region in the figure, if ABCD is a square of side 14 cm and APB and CPD are semicircles.
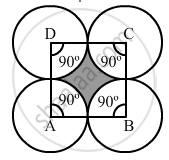
Four equal circles are described about the four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.
Find the volume and the surface area of the spheres in the following :
Diameter= 6.3 cm
There are two circular gardens A and B. The circumference of garden A is 1.760 km and the area of garden B is 25 times the area of garden A. Find the circumference of garden B.
The circumferences of two circles are in the ratio 5: 7, find the ratio between their radius.
The diameter of two circles are 28 cm and 24 cm. Find the circumference of the circle having its area equal to sum of the areas of the two circles.
The area between the circumference of two concentric circles is 2464cm2. If the inner circle has a circumference of 132cm, calculate the radius of the outer circle.
Ratio of circumference of a circle to its radius is always 2π:I.
