Advertisements
Advertisements
प्रश्न
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
उत्तर

Outer radius, r1 = 70 m
Inner radius, r2 = 63 m
∴ Area of track = `pir_1^2 - pir_2^2`
= `22/7[(70)^2 - (63)^2]`
= `22/7(70 + 63)(70 - 63)`
= `22/7 xx 133 xx 7`
= 2926 m2
Length of outer edge i.e. circumference
= `2pir_1`
= `2 xx 22/7 xx 70 = 440`m
Length of inner edge = `2pir_2`
= `2 xx 22/7 xx 63 = 396` m
Difference between lengths of two circumferences = 440 – 396 = 44 m
Hence (i) 2926 m2 (ii) 44 m
APPEARS IN
संबंधित प्रश्न
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
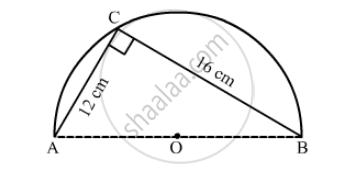
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
What is the area of a square inscribed in a circle of diameter p cm ?
A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum.
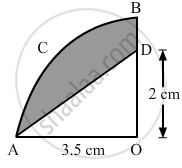
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
The minute hand of a clock is 12 cm long. Find the area swept by in it 35 minutes.
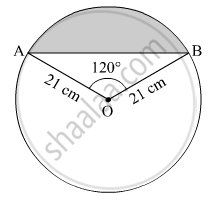
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
The length of the minute hand of a clock is 14 cm. The area swept by the minute hand in 5 minutes is ______.
Is the area of the circle inscribed in a square of side a cm, πa2 cm2? Give reasons for your answer.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
