Advertisements
Advertisements
Question
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
Solution
Let:
Length of each of the equal sides of the isosceles right-angled triangle = a = 10 cm
And.
Area of isosceles right – angled triangle=`1/2xxBasexxHeight`
The hypotenuse of an isosceles right – angled triangle can be obtained using Pythagoras’ theorem
If h denotes the hypotenuse, we have:
`h^2=a^2+a^2`
⇒`h=2a^2`
⇒`h=sqrt2a`
⇒`h=10sqrt2 cm``
∴ Perimeter of the isosceles right-angled triangle = `2a+sqrt2a`
=`2xx10+1.41xx10`
=`20+14.1`
=`34.1 cm`
APPEARS IN
RELATED QUESTIONS
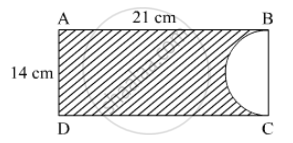
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
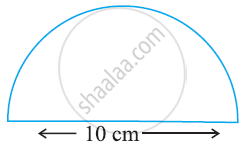
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
From a circular piece of cardboard of radius 3 cm two sectors of 900 have been cutoff . Find the perimeter of the remaining portion nearest hundredth centimeters ( `"Take" pi = 22/ 7`).
Write the area of the sector of a circle whose radius is r and length of the arc is l.
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then ______.
The area of a sector of a circle with radius r, making an angle of x° at the centre is
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
Diameter of a circular garden is 9.8 m. Find its area.
