Advertisements
Advertisements
Question
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
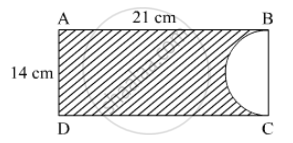
Solution
Area of the shaded region = Area of the rectangle − Area of the semicircle
`= 21 xx 14 - {1/2xx pi xx(14/2)^2}`
`=294 - {1/2 xx 22/7 xx 7 xx 7}`
= 297- 77
`= 217 cm^2`
Therefore area of shaded region is `217 cm^2`
= AB + AD + DC + BC
`= AB + AD + DC + 1/2 xx 2pi (14/2)`
`= 21 + 14 + 21 + 22/7 xx 7`
= 56 + 22
= 78 cm
Therefore the perimeter of the shaded region is 78 cm
APPEARS IN
RELATED QUESTIONS
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

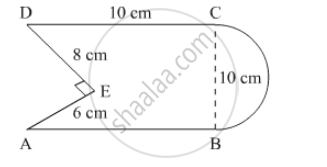
Find the area of the following figure, in square cm, correct to one place of decimal. (Take π = 22/7).
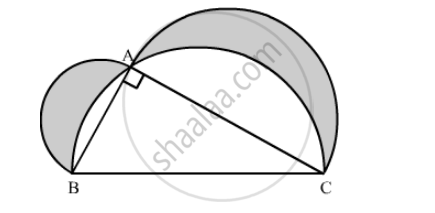
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
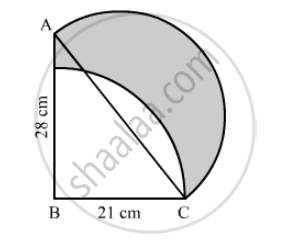
In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
The radii of two circles are in the ratio 5 : 8. If the difference between their areas is 156p cm2, find the area of the bigger circle.
The area of the circle whose diameter is 21 cm is ____________.
