Advertisements
Advertisements
Question
Each of the equal sides of an isosceles triangle measure 2 cm more than its height, and the base of the triangle measure 12 cm. Find the area of the triangle.
Solution
Let the height of the triangle be h cm.
Each of the equal sides measures `a=(h+2)cm and b=12 cm(base)`
Now, Area of the triangle = Area of the isosceles triangle
=`1/2xxbasexxheight=1/4xxbsqrt(4a^2-b^2)`
⇒ `1/2xx12xxh=1/4xx12xxsqrt(4(h+2)^2-144)`
⇒`6h=3sqrt(4h^2+16h-144)`
⇒`2h=sqrt(4h^2+16h+16-144)`
On squaring both the sides, we get:
⇒`4h^2=4h^2+16h+16-144`
⇒`16h-128=0`
⇒`h=8`
Area of the triangle=`1/2xxbxxh`
=`1/2xx12xx8`
=`48cm^2`
APPEARS IN
RELATED QUESTIONS
A 36-m-long, 15-m-borad verandah is to be paved with stones, each measuring 6dm by 5 dm. How many stones will be required?
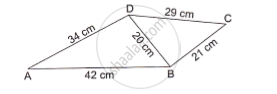
Find the area of the quadrilateral ABCD in which in AB=42 cm, BC=21 cm, CD=29cm, DA=34 cm and diagonal BD = 20 cm.
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
If the area of the circle is numerically equal to twice its circumference then what is the diameter of the circle?
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
On increasing the diameter of a circle by 40%, its area will be increased by
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
The sum of diameters of two circles is 112cm and the sum of their areas is 5236cm2. Find the radii of the two circles.
The length of the minute hand of a clock is 14 cm. The area swept by the minute hand in 5 minutes is ______.
Area of a quadrant of a circle of radius 7 cm is ______.
