Advertisements
Advertisements
प्रश्न
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
पर्याय
12 cm
16 cm
8 cm
10 cm
उत्तर
We have given length of the arc and area of the sector bounded by that arc and we are asked to find the radius of the circle.
If l is the length of the arc, A is the area of the arc and r is the radius of the circle, then we know the expression of the area of the sector in terms of the length of the arc and radius of the circle.
Area of the sector=`1/2 lr`
Now we will substitute the corresponding values of length of the arc and area of the sector.
`∴ 20 pi=1/2xx5pixxr`
Multiplying both sides of the equation by 2 we get,
`40pi=5pixxr`
Dividing both sides of the equation by `5pi`we get,
`r=8`
Therefore, radius of the circle is `8 cm`
APPEARS IN
संबंधित प्रश्न
Find the length of the diagonal of a square whose area is `128 cm^2` Also, find its perimeter.
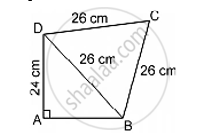
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
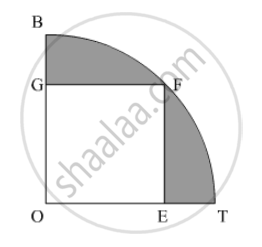
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
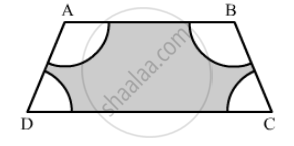
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use \[\pi = \frac{22}{7}\]
If diameter of a circle is increased by 40%, then its area increase by
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that ΔCEDis equilateral, then area of Δ ACE is
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is πb2 cm2? Why?
