Advertisements
Advertisements
प्रश्न
If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
पर्याय
2.2
1.1
9.625
96.25
उत्तर
Diameter of wheel (d) = 35 cm
Radius of wheel (r) = `"d"/2 = 35/2` cm
∴ The distance covered by the wheel in 1 revolution is equal to the circumference of the wheel = 2πr
= `2 × 22/7 × 35/2`
= `cancel2 × 22/(cancel(7)1) × (cancel(35)5)/cancel2`
= 22 × 5
= 110 cm
The distance covered by the wheel in one revolution (in m) is given by = `110/100` = 1.1 m
APPEARS IN
संबंधित प्रश्न
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
A road which is 7 m wide surrounds a circular park whose circumference is 352 m . Find the area of the road .
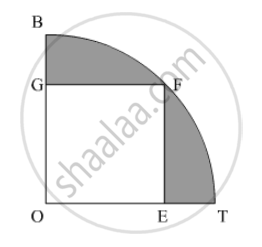
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

In the following figure, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.

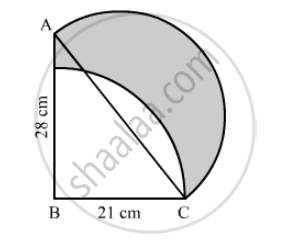
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
If diameter of a circle is increased by 40%, then its area increase by
The radii of the inner and outer circumferences of a circular running track are 63 m and 70 m respectively. Find :
(i) the area of the track ;
(ii) the difference between the lengths of the two circumferences of the track.
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
