Advertisements
Advertisements
प्रश्न
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
उत्तर
Given:
Radius = 2 cm
Angle of sector = 150°
Now,
Length of the arc`= (2pi"r"theta)/360`
`=(2xx22/7xx21xx150)/360`
= 55 cm
Area of the sector `= (pi"r"^2theta)/360`
`= 22/7xx21xx21xx150/360`
= 577.5 cm
APPEARS IN
संबंधित प्रश्न
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the large circle (in cm) is
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

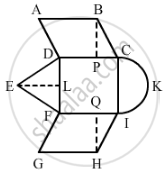
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
A square tank has an area of 1600 cm2. There are four semicircular plots around it. Find the cost of turfing the plots at Rs 12.50 per m2
The area of the circle whose diameter is 21 cm is ____________.
A table top is semicircular in shape with diameter 2.8 m. Area of this table top is ______.
