Advertisements
Advertisements
प्रश्न
A race track is in the form of a rig whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
उत्तर
Let r m and R m be the radii of the inner and outer tracks.
Now,
Circumference of the outer track = 2πR
`=> 396 = 2xx22/7xx"R"`
`=> "R" = (396xx7)/44`
⇒ R = 63
Circumference of the inner track = 2πr
`=> 352 = 2xx22/7xx"r"`
`=> r = (352xx7)/44 `
⇒ r = 56
Width of the track = Radius of the outer track -- Radius of the inner track
= 63 - 56
= 7 m
Area of the outer circle = πR2
`=22/7xx56xx56`
= 12474 m2
Area of the inner circle = πR2
`=22/7xx56xx56`
= 9856 m2
Area of the track = 12474 - 9856
= 2618 m2
APPEARS IN
संबंधित प्रश्न
If the circumference of a circular sheet is 154 m, find its radius. Also find the area of
the sheet. (Take `pi = 22/7`)
Find the diameter of the circle whose area is equal to the sum of the areas of two circles having radii 4 cm and 3 cm.
The circumference of a circle is 39.6 cm. Find its area.
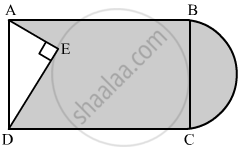
In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π = 3.14]
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has a circumference equal to the sum of circumferences of these two circles.
The radius of a circle is 21 cm. Find the circumference (Take π = `3 1/7`).
The cost of fencing a circular field at the rate of Rs.250 per metre is Rs.55000. The field is to be ploughing at the rate of Rs.15 per m2. Find the cost of ploughing the field.
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 56 m
Find the number of revolutions made by a circular wheel of area 1.54 m2 in rolling a distance of 176 m.
Circumference of a circle disc is 88 cm. Its radius is ______.
