Advertisements
Advertisements
प्रश्न
A race track is in the form of a rig whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
उत्तर
Let r m and R m be the radii of the inner and outer tracks.
Now,
Circumference of the outer track = 2πR
`=> 396 = 2xx22/7xx"R"`
`=> "R" = (396xx7)/44`
⇒ R = 63
Circumference of the inner track = 2πr
`=> 352 = 2xx22/7xx"r"`
`=> r = (352xx7)/44 `
⇒ r = 56
Width of the track = Radius of the outer track -- Radius of the inner track
= 63 - 56
= 7 m
Area of the outer circle = πR2
`=22/7xx56xx56`
= 12474 m2
Area of the inner circle = πR2
`=22/7xx56xx56`
= 9856 m2
Area of the track = 12474 - 9856
= 2618 m2
APPEARS IN
संबंधित प्रश्न
In Fig. 4, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
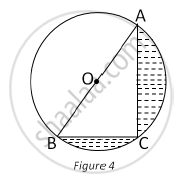
In Figure, find the area of the shaded region [Use π = 3.14]
A pendulum swings through an angle of 30º and describes an arc 8.8 cm in length. Find the length of the pendulum.
Find the circumference of the circle with the following radius: (Take `bb(pi = 22/7`)
21 cm
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Area of the circle
The area between the circumferences of two concentric circles is 2464 cm2. If the inner circle has circumference of 132 cm, calculate the radius of outer circle.
Find the area and perimeter of the following sector :
Radius= 4.2 cm, angle at the centre is 60 °
The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.
Find the radius of the circle whose circumference is equal to the sum of the circumferences of the circles having radius 15 cm and 8 cm.
Circumference of a circle of diameter 5 cm is ______.
