Advertisements
Advertisements
Question
In a grassland, a sheep is tethered by a rope of length 4.9 m. Find the maximum area that the sheep can graze
Solution
Length of the rope = 4.9 m
Area that the sheep can graze = Area of circle with radius 4.9 m
Area of the circle = πr2 sq.units
= `22/7 xx 4.9 xx 4.9`
= 22 × 0.7 × 4.9
= 75.46
∴ Area that the sheep can graze = 75.46 m2
APPEARS IN
RELATED QUESTIONS
Find the area of the following circle, given that diameter = 49 m.
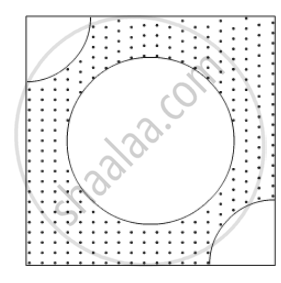
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
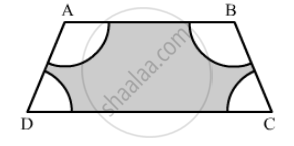
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use \[\pi = \frac{22}{7}\]
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
The radius of a wheel is 0.25 m. The number of revolutions it will make to travel a distance of 11 km will be
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
The area of a circle whose area and circumference are numerically equal, is
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
Find the areas of both the segments of a circle of radius 42 cm with central angle 120°.
The area of a circle is 1386 sq.cm; find its circumference.
