Advertisements
Advertisements
प्रश्न
Find the area of the sector of a circle having radius 6 cm and of angle 30°. [Take π = 3.14]
उत्तर
We have r = 6 cm and θ = 30°
Now, Area of sector`=theta/"360°"xxpi"r" = "30°"/"360°" xx 3.14xx36 = 9.42 "cm"^2 `
Hence, the area of the sector of the circles is 9.42 cm2 .
APPEARS IN
संबंधित प्रश्न
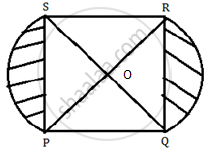
In the figure given below, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its
diagonals. Find the total area of the two flower beds (shaded parts).
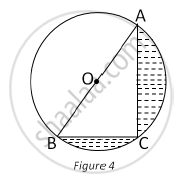
In Fig. 4, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
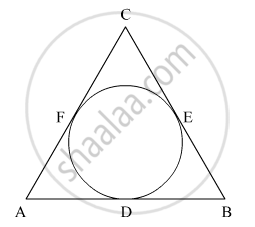
In Fig. 2, a circle is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA and 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF.
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days. (Take π = 22/7)
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour? [Use Π = 22/7]
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm. find the area of
- quadrant OACB
- the shaded region.
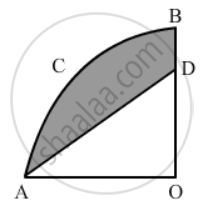
In Figure 2, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region.

Find the diameter of a circle whose circumference is equal to the sum of circumference of circles with radius 10 cm, 12 cm, and 18 cm.
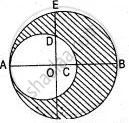
In the adjoining figure, the crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm, find the area of the shaded portion.