Advertisements
Advertisements
प्रश्न
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
उत्तर
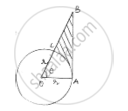
Given angle subtended at centre of circle = 𝜃
∠OAB = 90° [At joint of contact, tangent is perpendicular to radius]
OAB is right angle triangle
Cos 𝜃 =`(adj.side)/(hypotenuse) =r/OB`⇒ 𝑂𝐵 = 𝑟 sec 𝜃 … … (𝑖)
tan 𝜃 =`(opp.side)/(adju.side)=AB/r`⇒ 𝐴𝐵 = 𝑟 tan 𝜃 … … . (𝑖𝑖)
Area of shaded region = (area of triangle) – (area of sector)
`= (1/2× OA × AB) −theta/360^@× pir^2`
`=1/2× r × r tan theta −r^2/2[theta/180^@× pi]`
=`r^2/2[tantheta −(pitheta)/180]`
APPEARS IN
संबंधित प्रश्न
All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if the area of the circle is 1256 cm2. (Use π = 3.14)
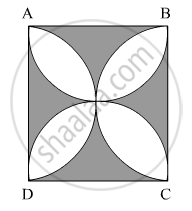
In Fig. 4, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
(use `pi=22/7`)
A wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
A steel wire when bent is the form of square encloses an area of 12 cm2. If the same wire is bent in form of circle. Find the area of circle.
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Length of arc
Find the total surface area and volume of a hemisphere whose radius is 10 cm.
The circumference of a circle is 440 cm. Find its radius and diameter. (Take π = `22/7`)
Using a ruler and compasses only:
(i) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ ABC = 120°.
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠ BCP.
The radius of a circle whose circumference is equal to the sum of the circumferences of the two circles of diameters 36 cm and 20 cm is ______.
Value of π is ______ approximately.
