Advertisements
Advertisements
प्रश्न
A horse is tied with a 21 m laig rope to the corner of a field which is in the shape of an equilateral triangle. Find the area of the field over which it can graze.
उत्तर
An equilateral triangle has all angles of 60 degrees
The horse will be able to graze over a sector of a circle of radius 21cm and angle 60, so
Area = `60^circ/360^circ pi "r"^2`
`= 60^circ/360^circ xx 22/7 xx 21 xx 21`
= 231 m2
Horse can graze in 231 m2
APPEARS IN
संबंधित प्रश्न
All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if the area of the circle is 1256 cm2. (Use π = 3.14)
In Fig. 4, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
(use `pi=22/7`)
If the perimeter of a semi-circular protractor is 66 cm, find the diameter of the protractor (Take π = 22/7).
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take `pi = 22/7`)
A sheet of paper is in the form of rectangle ABCD in which AB = 40cm and AD = 28 cm. A semicircular portion with BC as diameter is cut off. Find the area of remaining paper.
The circumference of two circles are in ratio 2:3. Find the ratio of their areas
The area of circle, inscribed in equilateral triangle is 154 cms2. Find the perimeter of
triangle.
Choose the correct alternative answer for the following question.
The curved surface area of a cylinder is 440 cm 2 and its radius is 5 cm. Find its height.
The circumference of a circle is 39.6 cm. Find its area.
A path of 8 m width runs around the outsider of a circular park whose radius is 17 m. Find the area of the path.
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
Four equal circles, each of radius a units, touch each other. Show that the area between them is `(6/7"a"^2)` sq units.
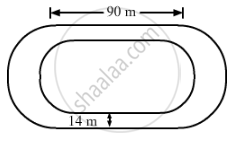
The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.
Each wheel of a car is of diameter 80 cm. How many completer revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour?
The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width of 3.5 m. Find the area of the path.
Find the dimensions of a rectangular park whose perimeter is 60 m and area 200 m2.
A cart wheel makes 9 revolutions per second. If the diameter of the wheel is 42cm, find its speed in km per hour. (Answer correct to the nearest km)
A ground is in the form of a circle whose diameter is 350 m. An athlete makes 4 revolutions. Find the distance covered by the athlete
In covering a distance s metres, a circular wheel of radius r metres makes `s/(2πr)` revolutions. Is this statement true? Why?
