Advertisements
Advertisements
प्रश्न
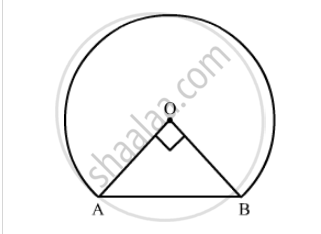
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by chord AB.
उत्तर
We have to find the area of the sector AOB formed by the chord AB.
We have `OA=4 cm and AB=4 cm. So,`
`AL=(AB)/2 cm`
`= 4/2 cm`
`= 2 cm`
Let ∠AOB=2θ. then,
`∠AOL=∠BOL`
=θ
In ΔOLA, We have
`sin θ=(AL)/(OA)`
`= 2/4`
`=1/2`
`θ = sin^-1 1/2`
`= 30°`
Hence, `∠AOB=60°`
Now, using the value of`∠AOB` and r we will find the area of sector AOB,
`A=θ/(360°) xx pir^2`
=` (60°)/(360°)xx pixx4xx4 cm^2`
`=(8pi)/3 cm^2`
`
APPEARS IN
संबंधित प्रश्न
A room is 16 m long and 13.5 m broad. Find the cost of covering its floor with 75-m-wide carpet at ₹ 60 per metre.
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
In the following figure, PQRS is a square of side 4 cm. Find the area of the shaded square.
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
If the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector? (Take \[\pi = 22/7\])
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
The area of a sector whose perimeter is four times its radius r units, is
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
The length of an arc of the sector of angle θ° of a circle with radius R is
