Advertisements
Advertisements
Question
The diameters of the front and rear wheels of a tractor are 80 cm and 2 m respectively. Find the number of revolutions that a rear wheel makes to cover the distance which the front wheel covers is 800 revolutions.
Solution
Radius of the front wheel = 40 cm = 2/5 m
Circumference of the front wheel `= (2pixx2/5)"m" = (4pi)/5 "m"`
Distance covered by the front wheel in 800 revolutions `=((4pi)/5 xx800)"m" = (640pi)"m"`
Radius of the rear wheel = 1 m
Circumference of the rear wheel `= (2pixx1) =2pi "m" `
∴ Required number of revolutions `"=Distance covered by the front wheel in 800 revolutions"/"Circumference of the rear wheel"`
`= (640pi)/(2pi)`
= 320
APPEARS IN
RELATED QUESTIONS
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Find the area of a right – angled triangle, the radius of whose, circumference measures 8 cm and the altitude drawn to the hypotenuse measures 6 cm.
Find the area of the rhombus, the length of whose diagonals are 30 cm and 16 cm. Also, find the perimeter of the rhombus.
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is not bent in the form of a circle. Find the area enclosed by the circle.
The difference between the circumference and radius of a circle is 37 cm. The area of the circle is
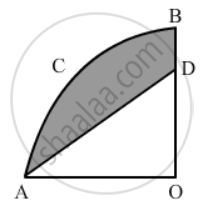
OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm. find the area of
- quadrant OACB
- the shaded region.
Find the area and perimeter of the circle with the following :
Diameter = 77 cm
The shaded portion of the figure, given alongside, shows two concentric circles. If the circumference of the two circles is 396 cm and 374 cm, find the area of the shaded portion.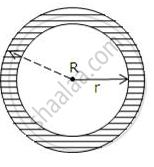
The diameter of a circular field is 56 m. Find its circumference and cost of fencing it at the rate of ₹80 per m. (Take π =`22/7`)
Find the area and perimeter of the following semicircles: Radius = 1.4cm
