Advertisements
Advertisements
Question
Four equal circles, each of radius 5 cm touch each other as shown in fig. Find the area included etween them.
Solution
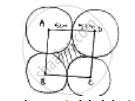
Area required shaded = (area of square ABCD) – (Area of 4 quadrant)
Side of square = 5cm + 5cm
= 10cm
Area of square = side × side
= 10๐๐ × 10๐๐ = 100๐๐2
Area of quadrant =`1/4` (๐๐๐๐ ๐๐ ๐๐๐๐๐๐ ๐ค๐๐กโ ๐๐๐๐๐ข๐ 5 ๐๐)
=`1/4×pir^2`
=`1/4×22/7× 5 × 5 = (25 × 3.14) 1/4 cm^2`
Area included between circles = (area of square) – 4(area of quadrant)
= `100 – (1/4× 25 × 2.14)`
= 100 – 78.5
= 21.5cm2
APPEARS IN
RELATED QUESTIONS
All the vertices of a rhombus lie on a circle. Find the area of the rhombus, if the area of the circle is 1256 cm2. (Use π = 3.14)
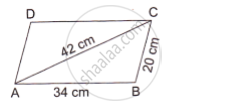
The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then ______.
Find the area enclosed between two concentric cirdes of radii 6.3 cm and 8.4 cm. A third concentric circle is drawn outside the 8.4 cm circle, so that the area enclosed between it and 8.4 cm cirde is the same as that between two inner circles. Find the radii of the third circle correct to two decimal places .
A metal wire, when bent in the form of an equilateral triangle of largest area, encloses an area of 484 `sqrt3` cm2. If the same wire is bent into the form of a circle of largest area, find the area of this circle.
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has a circumference equal to the sum of circumferences of these two circles.
Construct the circumcircle of the ABC when BC = 6 cm, B = 55° and C = 70°.
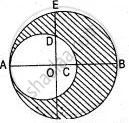
In the adjoining figure, the crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm, find the area of the shaded portion.
Find the area and perimeter of the following semicircles: Diameter = 5.6cm
The area of a square is 100 cm2. The circumference (in cm) of the largest circle cut of it is ______.
