Advertisements
Advertisements
प्रश्न
Find the area of the shaded region in figure, where arcs drawn with centres A, B, C and D intersect in pairs at mid-points P, Q, R and S of the sides AB, BC, CD and DA, respectively of a square ABCD (Use π = 3.14).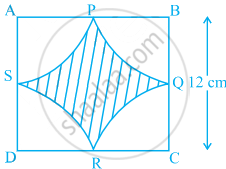
उत्तर
Given, side of a square BC = 12 cm
Since, Q is a mid-point of BC.
∴ Radius = BQ = `12/2` = 6 cm
Now, area of quadrant BPQ
= `(pi"r"^2)/4`
= `(3.14 xx (6)^2)/4`
= `113.04/4 "cm"^2`
Area of four quadrants
= `(4 xx 113.04)/4`
= 113.04 cm2
Now, area of square ABCD
= (12)2
= 144 cm2
∴ Area of the shaded region
= Area of square – Area of four quadrants
= 144 – 113.04
= 30.96 cm2
APPEARS IN
संबंधित प्रश्न
Tick the correct answer in the following and justify your choice: If the perimeter and the area of a circle are numerically equal, then the radius of the circle is:
If the circumference of a circle and the perimeter of a square are equal, then ______.
If the perimeter of a circle is equal to that of a square, then the ratio of their areas is ______.
Is it true to say that area of a square inscribed in a circle of diameter p cm is p2 cm2? Why?
Will it be true to say that the perimeter of a square circumscribing a circle of radius a cm is 8a cm? Give reasons for your answer.
The radius of a circle is same as the side of a square. Their perimeters are in the ratio
