Advertisements
Advertisements
Question
A car has two wipers which do not overlap. Each wiper has blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades [Use π = `22/7`]
Solution
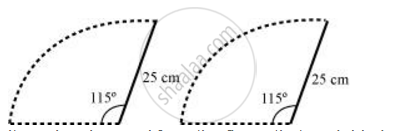
It can be observed from the figure that each blade of wiper will sweep an area of a sector of 115° in a circle of 25 cm radius.
Area of such sector = `115^@/360^@ xx pi xx (25)^2`
`= 23/72 xx 22/7 xx 25 xx 25`
`= 158125/252 "cm"^2`
Area swept by 2 blades = `2xx 158125/252`
`= 158125/126 "cm"^2`
APPEARS IN
RELATED QUESTIONS
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).
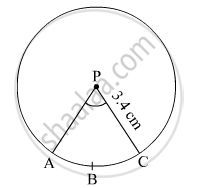
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
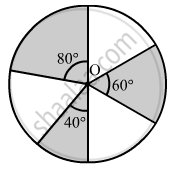
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
Find the perimeter of a quadrant of a circle of radius 14 cm.
