Advertisements
Advertisements
Questions
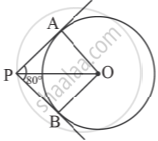
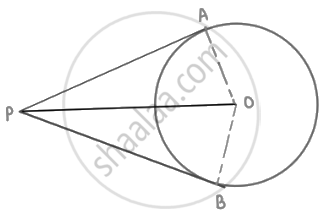
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
If tangents PA and PB drawn from an external point P to the circle with centre O are inclined to each other atan angle of 80° as shown in the given figure, then the measure of ∠POA is ______.
Options
50°
60°
70°
80°
40°
Solution
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to 50°.
Explanation:
It is given that PA and PB are tangents.

Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
Thus, OA ⊥ PA and OB ⊥ PB
∠OBP = 90º
∠OAP = 90º
In AOBP,
Sum of all interior angles = 360°
∠OAP + ∠APB + ∠PBO + ∠BOA = 360°
⇒ 90° + 80° + 90° + ∠BOA = 360°
⇒ 260° + ∠BOA = 360°
⇒ ∠BOA = 360° – 260°
⇒ ∠BOA = 100°
In ΔOPB and ΔOPA,
AP = BP (Tangents from a point)
OA = OB (Radii of the circle)
OP = OP (Common side)
Therefore, ΔOPB ≅ ΔOPA (SSS congruence criterion)
A ↔ B, P ↔ P, O ↔ O
And thus, ∠POB = ∠POA
`angle"POA" = 1/2 angle"AOB" = (100^@)/2 = 50^@`
Hence, alternative 50° is correct.
RELATED QUESTIONS
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

Prove that the lengths of the tangents drawn from an external point to a circle are equal.
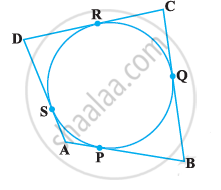
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
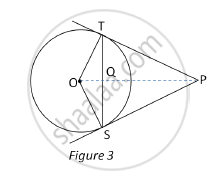
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
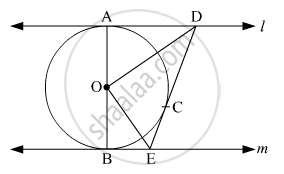
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
The length of tangents drawn from an external point to the circle ______
The number of tangents drawn at a point of the circle is/are ______
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

The length of the tangent from an external point on a circle is ______
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
The angle between two tangents to a circle may be 0°.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
The length of tangent from an external point P on a circle with centre O is always less than OP.
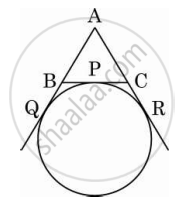
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.