Advertisements
Advertisements
Question
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
Options
45°
30°
90°
60°
Solution
60°
Explanation;
Hint:
Ratio of length of the tower : length of the shadow = `sqrt(3): 1`
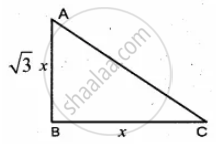
Let the tower be `sqrt(3)` x and the shadow be x
tan C = `"AB"/"BC"`
⇒ tan C = `(sqrt(3)x)/x =sqrt(3)`
tan C = tan 60°
⇒ ∴ ∠C = 60°
APPEARS IN
RELATED QUESTIONS
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
