Advertisements
Advertisements
Question
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
Solution
Let the radius and height of the bigger cone be R and H, respectively.
Given: H = 30 cm
Let the radius and height of the smaller cone be r and h, respectively.
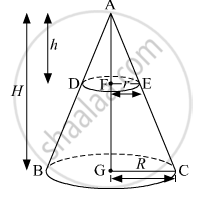
Now, in ∆AFE and ∆AGC,
∠AEF = ∠ACG (Corresponding angles)
∠AFE = ∠AGC (90°° each)
∴∆AFE~∆AGC (AA similarity)
\[\Rightarrow \frac{AF}{AG} = \frac{FE}{GC}\]
\[ \Rightarrow \frac{h}{H} = \frac{r}{R} . . . . . \left( 1 \right)\]
It is given that
Volume of the smaller cone \[\frac{1}{27} \times\] Volume of the bigger cone
\[\Rightarrow \frac{1}{3}\pi r^2 h = \frac{1}{27} \times \frac{1}{3}\pi R^2 H\]
\[ \Rightarrow \left( \frac{r}{R} \right)^2 \times \frac{h}{H} = \frac{1}{27}\]
\[ \Rightarrow \left( \frac{h}{H} \right)^2 \times \frac{h}{H} = \frac{1}{27} \left[ Using \left( 1 \right) \right]\]
\[ \Rightarrow \left( \frac{h}{H} \right)^3 = \frac{1}{27}\]
\[ \Rightarrow \frac{h}{H} = \frac{1}{3}\]
Now,
FG = AG − AF = 30 cm − 10 cm = 20 cm
Hence, the section is made 20 cm above the base.
APPEARS IN
RELATED QUESTIONS
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30º. The distance of the car from the tower (in metres) is
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
