Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
उत्तर
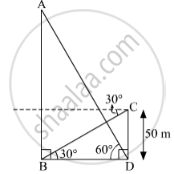
Let AB be the hill and CD be the tower.
Angle of elevation of the hill at the foot of the tower is 60°, i.e., ∠ADB = 60° and the angle of depression of the foot of hill from the top of the tower is 30°, i.e., ∠CBD = 30°.
Now in right angled ΔCBD:
`tan30^@=(CD)/(BD)`
`rArrBD=(CD)/tan30^@`
`rArrBD=50/((1/sqrt3))`
`rArrBD =50sqrt3`
In right ΔABD:
`tan60^@=(AD)/(BD)`
`rArr AB=BDxxtan60^@`
`=50sqrt3xxsqrt3m`
`=50xx3m`
`=150m`
Hence, the height of the hill is 150 m.
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
A kite is flying at a height of 45 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is
60°. Find the length of the string assuming that there is no slack in the string.
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30º. The distance of the car from the tower (in metres) is
In figure given ABCD is a rectangle, the value of CE is ____________.

If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
