Advertisements
Advertisements
Question
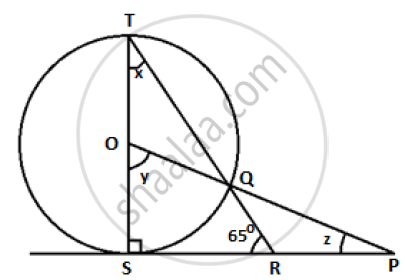
In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°,
find the value of x, y and z.

Solution
In the given figure, TS ⊥ SP,
m∠TSR = m∠OSP = 90°
In `triangle TSR, m angleTSR + m angleTSR + m angle RTS = 180^@`
`=> 90^@ + 65^@ + x = 180^@`
`=> x = 180^@ - 90^@ - 65^@`
`=> x= 25^@`
Now, y = 2x [Angle subtended at the centre is double that of the angle subtended by the arc at the same centre]
`=> y = 2 xx 25^@`
`:. y = 50^@`
In `triangle OSP ,m angleOSP + m angle SPO + m angle POS =180^@`
`=> 90^@ + z + 50^@ = 180^@`
`=> z = 180^@ - 140^@`
`:. z=40^@`
APPEARS IN
RELATED QUESTIONS
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC and measure its radius.
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw a circle with center O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Draw a circle of radius 4 cm. From a point 6 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.
Draw a circle of radius 3 cm. Construct a square about the circle.
A pair of tangents can be constructed from a point P to a circle of radius 3.5 cm situated at a distance of 3 cm from the centre.
