Advertisements
Advertisements
प्रश्न
- Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm.
- Find its in centre and mark it I.
- With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle. What is the length of the radius of this circle.
उत्तर
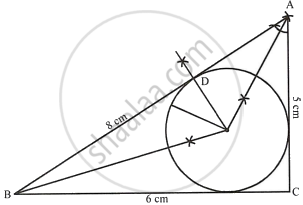
Steps of construction:
- Draw a line segment BC = 6 cm.
- With centre B and radius 8 cm draw an arc.
- With centre C and radius 5 cm draw another arc which intersects the first arc at A.
- Join AB and AC.
ΔABC is the required triangle. - Draw the angle bisectors of ∠B and ∠A intersecting each other at I. Then I is the incentre of the triangle ABC.
- Through I, draw ID ⊥ AB.
- Now from D, cut off `DP = DQ = 2/2 = 1 cm`.
- With centre I and radius IP or IQ, draw a circle which will intersect each side of triangle ABC cutting chords of 2 cm each.
APPEARS IN
संबंधित प्रश्न
Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle.Steps
Draw a circle of radius 3 cm. Take a point at a distance of 5.5 cm from the centre of the circle. From point P, draw two tangents to the circle.
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between the tangents is 45°.
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°.
Draw a circle of radius 4 cm and take a point Pon its circumference. Construct a tangent to the circle at P.
Draw a circle of radius 4 cm. From a point 6 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
You are given a circle with radius ‘r’ and center O. You are asked to draw a pair of tangents which are inclined at an angle of 60° with each other. Refer to the figure and select the option which would lead us to the required construction. d is the distance OE.

