Advertisements
Advertisements
Question
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
Options
6 cm
8 cm
10 cm
12 cm
Solution
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is 10 cm.
Explanation:
Given in the question, AB = 12 cm and BC = 16 cm.
In a circle, BC ⊥ AB. So, that means AC will be a diameter of circle.
Now, by using Pythagoras theorem in right-angled triangle ABC.
AC2 = AB2 + BC2
AC2 = (12)2 + (16)2
AC2 = 144 + 256
AC2 = 400
AC = 20 cm
So, radius of circle = `1/2 xx AC`
= `1/2 xx 20`
= 10 cm
Therefore, the radius of circle is 10 cm.
APPEARS IN
RELATED QUESTIONS
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Use the figure given below to fill in the blank:
Diameter = 2 x ________

Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
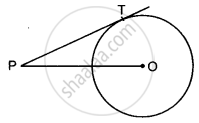
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
