Advertisements
Advertisements
प्रश्न
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
उत्तर
Join OB, OC and OA.
In ∆ABO and ∆ACO,
AB = AC ...[Given]
BO = CO ...[Radii of same circle]
AO = AO ...[Common side]
∴ ∆ABO ≅ ∆ACO ...[By SSS congruence criterion]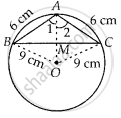
⇒ ∠1 = ∠2 ...[CPCT]
Now, In ∆ABM and ∆ACM,
AB = AC ...[Given]
∠1 = ∠2 ...[Proved above]
AM = AM ...[Common side]
∴ ∆AMB ≅ ∆AMC ...[By SAS congruence criterion]
⇒ ∠AMB = ∠AMC ...[CPCT]
Also, ∠AMB + ∠AMC = 180° ...[Linear pair]
⇒ ∠AMB = 90°
We know that a perpendicular from the centre of circle bisects the chord.
So, OA is a perpendicular bisector of BC.
Let AM = x, then OM = 9 – x ...[∵ OA = radius = 9 cm]
In right angle ∆AMC,
AC2 = AM2 + MC2 ...[By Pythagoras theorem]
⇒ MC2 = 62 – x2 …(i)
In right angle ∆OMC,
OC2 = OM2 + MC2 ...[By Pythagoras theorem]
⇒ MC2 = 92 – (9 – x)2
From equation (i) and (ii),
62 – x2 = 92 – (9 – x)2
⇒ 36 – x2 = 81 – (81 + x2 – 18x)
⇒ 36 = 18x
⇒ x = 2
∴ AM = 2 cm
From equation (ii),
MC2 = 92 – (9 – 2)2
⇒ MC2 = 81 – 49 = 32
⇒ MC = `4sqrt(2)` cm
∴ BC = 2 MC = `8sqrt(2)` cm
∴ Area of ∆ABC = `1/2` × Base × Height
= `1/2 xx "BC" xx "AM"`
= `1/2 xx 8sqrt(2) xx 2`
= `8sqrt(2) "cm"^2`
Hence, the required area of ∆ABC is `8sqrt(2) "cm"^2`.
APPEARS IN
संबंधित प्रश्न
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
ture or false v
The degree measure of a semi-circle is 180°.
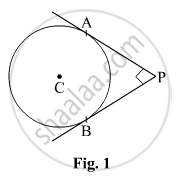
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
Find the diameter of the circle
Radius = 10 cm
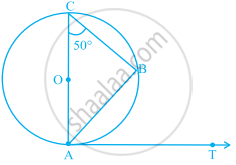
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
