Advertisements
Advertisements
Question
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Solution
Correct answer: D
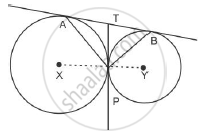
TA = TP ⇒ ∠TAP = ∠TPA
TB = TP ⇒∠TBP = ´TPB
∠TAP + ∠TBP
Correct answer: D

TA = TP ⇒ ∠TAP = ∠TPA
TB = TP ⇒∠TBP = ´TPB
∠TAP + ∠TBP= ∠TPA + ∠TPB= ∠APB
` ∠TAP + ∠TBP+ ∠APB=180^@[because "sum of" ......180^@]`
`/_APB+/_APB=180^@`
`2/_APB=180^@`
`/_APB=90^@`
APPEARS IN
RELATED QUESTIONS
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
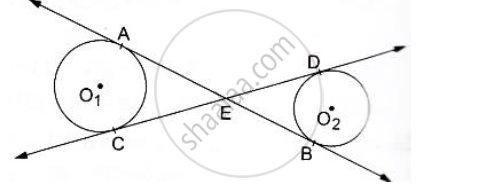
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.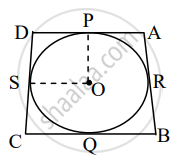
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
In the given figure, O is the centre of the circle. Name all chords of the circle.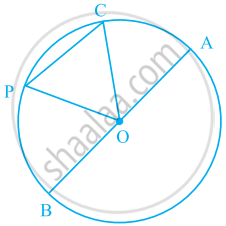
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
