Advertisements
Advertisements
प्रश्न
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
पर्याय
- \[\frac{BC}{DF} = \frac{AC}{DE}\]
- \[\frac{AB}{DE} = \frac{BC}{DF}\]
- \[\frac{AB}{EF} = \frac{AC}{DE}\]
- \[\frac{BC}{DF} = \frac{AB}{EF}\]
उत्तर
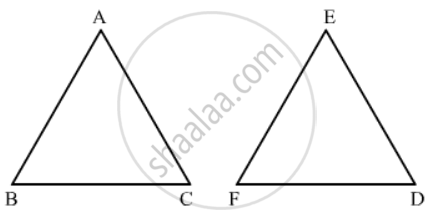
In ΔABC and ΔDEF
`∠ A = ∠ E`
`∠ B = ∠ F`
∴ ΔABC and ΔDEF are similar triangles.
Hence `(AB)/(EF)=(BC)/(FD)=(CA)/(DE)`
Hence the correct answer is (b).
APPEARS IN
संबंधित प्रश्न
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

In the below figure, If AB || CD, find the value of x.
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
If ∆ABC and ∆DEF are two triangles such that\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{3}{4}\], then write Area (∆ABC) : Area (∆DEF)
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
