Advertisements
Advertisements
प्रश्न
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
विकल्प
\[\frac{13}{2}cm\]
- \[\frac{60}{13}cm\]
- \[\frac{13}{60}cm\]
- \[\frac{2\sqrt{15}}{13}cm\]
उत्तर
Given: In ΔABC `∠ A=90^o, AD⊥ BC`,, AC = 12cm, and AB = 5cm.
To find: AD
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
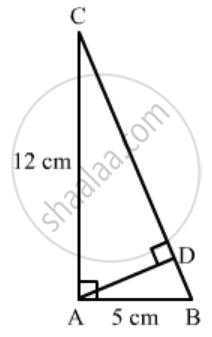
In ∆ACB and ∆ADC,
APPEARS IN
संबंधित प्रश्न
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

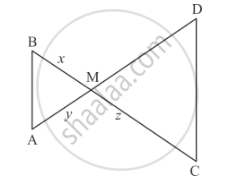
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
In ∆ABC, ∠A = 60°. Prove that BC2 = AB2 + AC2 − AB . AC.
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
In an equilateral triangle ABC if AD ⊥ BC, then
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
