Advertisements
Advertisements
प्रश्न
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
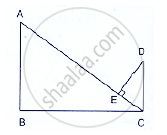
उत्तर
Given: AB ⊥ BC, DC ⊥ BC and DE ⊥ AC
To prove: ΔCED ~ ΔABC
Proof:
∠BAC + ∠BCA = 90° …(i) [By angle sum property]
And, ∠BCA + ∠ECD = 90° …(ii) [DC ⊥ BC given]
Compare equation (i) and (ii)
∠BAC = ∠ECD …(iii)
In ΔCED and ΔABC
∠CED = ∠ABC [Each 90°]
∠ECD = ∠BAC [From (iii)]
Then, ΔCED ~ ΔABC [By AA similarity]
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
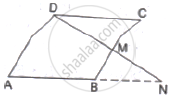
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

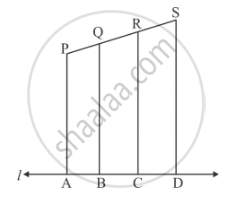
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
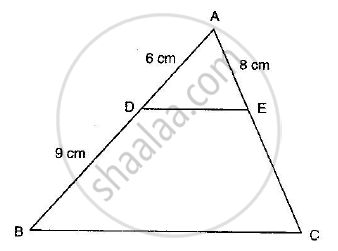
In the adjoining figure, find AC.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
