Question

D, E and F are the points on sides BC, CA and AB respectively of ΔABC such that AD bisects ∠A, BE bisects ∠B and CF bisects ∠C. If AB = 5 cm, BC = 8 cm and CA = 4 cm, determine AP, CE and BD.

Answer 1

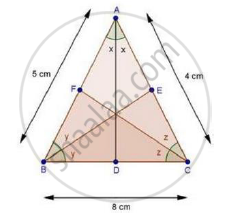
In ΔABC, CF bisects ∠C.

We know that, the internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.

`therefore"AF"/"FB"="AC"/"BC"`

`rArr"AF"/(5-"AF")=4/8`       [∵ FB = AB – AF = 5 – AF]

`rArr"AF"/(5-"AF")=1/2`

⇒ 2AF = 5 – AF

⇒ 2AF + AF = 5

⇒ 3AF = 5

`rArr"AF"=5/3` cm

Again, In ΔABC, BE bisects ∠B.

`therefore"AE"/"EC"="AB"/"BC"`

`rArr(4-"CE")/"CE"=5/8`     [∵ AE = AC – CE = 4 – CE]

⇒ 8(4 − 𝐶𝐸) = 5 × CE

⇒ 32 – 8CE = 5CE

⇒ 32 = 13CE

`rArr"CE"=32/13` cm

Similarly,

`"BD"/"DC"="AD"/"AC"`

`rArr"BD"/(8-"BD")=5/4`        [∵ DC = BC – BD = 8 – BD]

⇒ 4BD = 40 – 5BD

⇒ 9BD = 40

`rArr"BD"=40/9` cm

Hence, `AF=5/3` cm, `"CE"=32/13` cm and `"BD"=40/9` cm.