Advertisements
Advertisements
Question
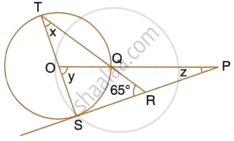
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
Solution
TS ⊥ SP,
`=>` ∠TSR = 90°
In ΔTSR,
∠TSR + ∠TRS + ∠RTS = 180°
`=>` 90° + 65° + x = 180°
`=>` x = 180° – 90° – 65°
`=>` x = 25°
Now, y = 2x ...(Angle subtended at the center is double that of the angle subtended by the arc at the same centre)
`=>` y = 2 × 25°
`=>` y = 50°
In ΔOSP,
∠OSP + ∠SPO + ∠POS = 180°
`=>` 90° + z + 50° = 180°
`=>` z = 180° – 140°
`=>` z = 40°
Hence, x = 25°, y = 50° and z = 40°
APPEARS IN
RELATED QUESTIONS
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
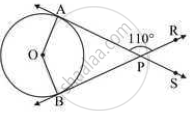
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
The number of tangents drawn at a point of the circle is/are ______
The length of the tangent from an external point P on a circle with centre O is ______
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).