Advertisements
Advertisements
प्रश्न
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
उत्तर
OP = 2r
Tangents drawn from external point to the circle are equal in length
PA = PB
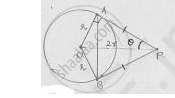
At point of contact, tangent is perpendicular to radius.
In ΔAOP, sin 𝜃 =`"opp.side"/"hypotenuse"=r/(2r)=1/2`
𝜃 = 30°
∠APB = 20 = 60°, as PA = PB ∠BAP = ∠ABP = x.
In ΔPAB, by angle sum property
∠APB + ∠BAP + ∠ABP = 180°
2x = 120° ⇒ x = 60°
In this triangle all angles are equal to 60°
∴ ΔAPB is equilateral.
APPEARS IN
संबंधित प्रश्न
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.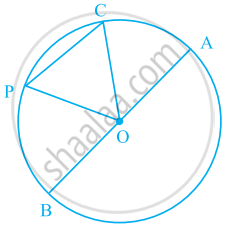
From the figure, identify the centre of the circle.
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
