Advertisements
Advertisements
प्रश्न
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

उत्तर
In cyclic quadrilateral ABCD,
∠B + ∠D = 180° (opp angles of the cyclic quad are supplementary)
⇒ 100° + ∠ADC = 180°
=> ∠ADC = 80°
Now in ΔACD
∠ACD + ∠CAD + ∠ADC = 180°
40° + ∠CAD + 80° = 180°
∠CAD = 180° - 120° = 60°
Now ∠DCT = ∠CAD (angles in the alternate segment)
∴ ∠DCT = 60°
APPEARS IN
संबंधित प्रश्न
The common point of a tangent to a circle and the circle is called ______.
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
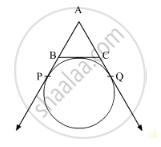
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
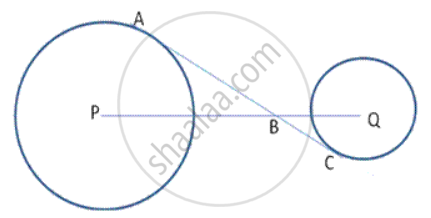
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
Find the value of ∠DCE.

ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______


In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
