Question

In the given diagram, ΔADB and ΔACB are two right-angled triangles with ∠ADB = ∠BCA = 90°. If AB = 10 cm, AD = 6 cm, BC = 2.4 cm and DP = 4.5 cm.

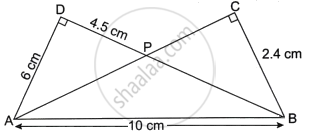
1. Prove that ΔAPD ∼ ΔBPC
2. Find the length of BD and PB
3. Hence, find the length of PA
4. Find area ΔAPD : area ΔBPC.

Answer 1

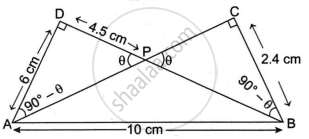
Given: In ΔADB and ΔACB,

∠ADB = ∠BCA = 90°

AB = 10 cm, AD = 6 cm, BC = 2.4 cm, DP = 4.5 cm

a. In ΔAPD and ΔBPC

∠APD = ∠BPC    ...(Vertically opposite angles)

∠ADP = ∠BCP = 90°

∴ ΔAPD ∼ ΔBCP    ...(By AA similarity criterion)

b. In ΔABD,

By Pythagoras’ theorem,

AB² = AD² + BD²

(10)² = 6² + (BD)²

BD² = 100 – 36 = 64

BD = 8 cm

Then, PB = BD – PD

= 8 – 4.5

= 3.5 cm

c. In ΔPAD,

By Pythagoras’ theorem,

AP² = AD² + PD²

AP² = 6² + (4.5)²

= 36 + 20.25

= 56.25

AP = `sqrt(56.25)` cm

AP = 7.5 cm

d. Since, ΔAPD ∼ ΔBPC

∴ `(ar(ΔAPD))/(ar(ΔBPC)) = (AD^2)/(BC^2)`

= `(6 xx 6)/(2.4 xx 2.4)`

= `(1 xx 1)/(0.4 xx 0.4)`

= `(10 xx 10)/(4 xx 4)`

= `25/4`

Hence, ar(ΔAPD) : ar(ΔBPC) = 25 : 4