Advertisements
Advertisements
प्रश्न
Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
उत्तर
Here, ABCD is a cyclic quadrilateral.
PM is the bisector of ∠ APB and QM is a bisector of ∠ AQD.
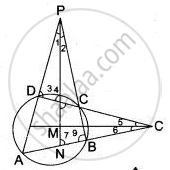
In Δ PDL and Δ PBN,
∠ 1 = ∠ 2 ...( PM is the bisector of ∠P )
∠ 3 = ∠ 9 ...( Exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.)
∠ 4 = ∠ 7
But, ∠ 4 = ∠ 8 ...( Vertically opposite angles)
∠ 7 = ∠ 8
Now in Δ QMN and Δ QML,
∠ 7 = ∠ 8 ...(prove above)
∠ 5 = ∠ 6 ...( QM is a bisector of Q)
Δ QMN ∼ Δ QML
∠ QMN = ∠ QML
But
∠ QMN + ∠ QML = 180°
∠ QMN = ∠ QML = 90°
Hence, ΔPMQ = 90° ...( ∵ ∠PMQ = ∠QML)
Hence proved.
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

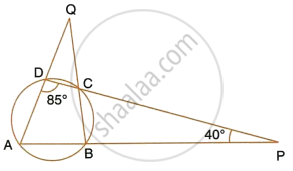
Use the given figure to find:
- ∠BAD,
- ∠DQB.
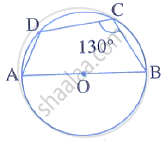
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
