Advertisements
Advertisements
प्रश्न
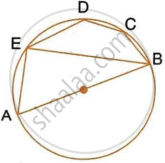
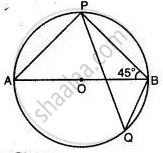
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
उत्तर
1) In ΔABD, ∠DAB + ∠ABD + ∠ADB = 180°
⇒ 65° + 70° + ∠ADB = 180°
⇒ ∠ADB = 180° - 70° - 65° = 45°
Now, ∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°
⇒ ∠ADC is the angle of semi-circle
So, AC is a diameter of the circle.
2) ∠ACB = ∠ADB (angle subtended by the same segment)
∠ACB = 45°
APPEARS IN
संबंधित प्रश्न
Prove that the parallelogram, inscribed in a circle, is a rectangle.
Prove that the rhombus, inscribed in a circle, is a square.
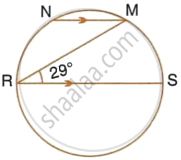
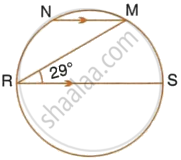
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.
Calculate:
- ∠EBA,
- ∠BCD.
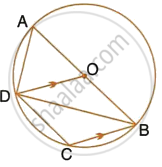
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate:
- ∠DAB,
- ∠DBA,
- ∠DBC,
- ∠ADC.
Also, show that the ΔAOD is an equilateral triangle.
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
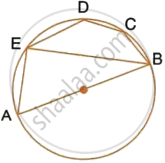
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
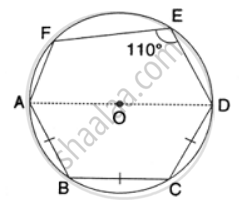
In the following figure, AD is the diameter of the circle with centre O. chords AB, BC and CD are equal. If ∠DEF = 110°, Calculate: ∠FAB.
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
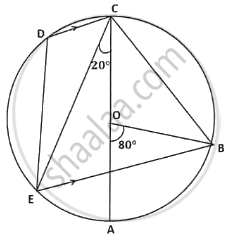
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED