Advertisements
Advertisements
प्रश्न
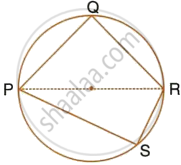
The following figure shows a circle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, find the perimeter of the cyclic quadrilateral PQRS.
उत्तर
In the figure, PQRS is a cyclic quadrilateral in which PR is a diameter
PQ = 7 cm
QR = 3RS = 6 cm
3RS = 6 cm
RS = 2 cm
Now in ∆PQR,
∠Q = 90° ...[Angles in a semi-circle]
∴ PR2 = PQ2 + QR2 ...[Pythagoras theorem]
= 72 + 62
= 49 + 36
= 85
Again in right ΔPSQ,
PR2 = PS2 + RS2
`=>` 85 = PS2 + 22
`=>` PS2 = 85 – 4 = 81 = (9)2
∴ PS = 9 cm
Now, perimeter of quad PQRS
= PQ + QR + RS + SP
= (7 + 9 + 2 + 6) cm
= 24
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
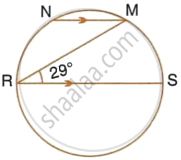
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM
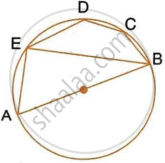
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.
Calculate:
- ∠EBA,
- ∠BCD.
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF
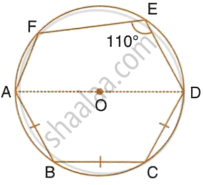
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
Using ruler and a compass only construct a semi-circle with diameter BC = 7cm. Locate a point A on the circumference of the semicircle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure ∠ADC and write it down.
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
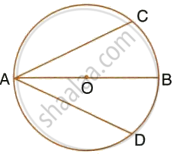
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.
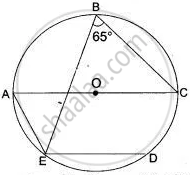
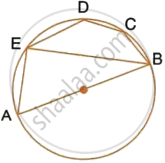
In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.