Advertisements
Advertisements
प्रश्न
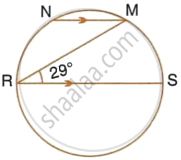
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM
उत्तर

Join RN and MS.
∴ ∠RMS = 90°
(Angle in a semicircle is a right angle)
∴ ∠RSM = 90° – 29° = 61°
(By angle sum property of triangle RMS)
∴ ∠RNM = 180° ∠RSM = 180° – 61° = 119°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
APPEARS IN
संबंधित प्रश्न
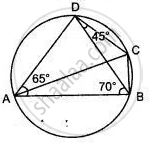
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Calculate the area of the shaded region, if the diameter of the semicircle is equal to 14 cm. Take `pi = 22/7`

Prove that the parallelogram, inscribed in a circle, is a rectangle.
In the figure, given alongside, AB || CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Using ruler and a compass only construct a semi-circle with diameter BC = 7cm. Locate a point A on the circumference of the semicircle such that A is equidistant from B and C. Complete the cyclic quadrilateral ABCD, such that D is equidistant from AB and BC. Measure ∠ADC and write it down.
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.
In the figure, ∠DBC = 58°. BD is diameter of the circle.
Calculate:
- ∠BDC
- ∠BEC
- ∠BAC
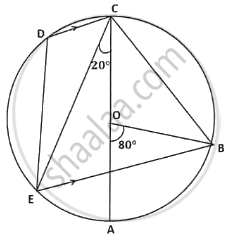
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED