Advertisements
Advertisements
प्रश्न
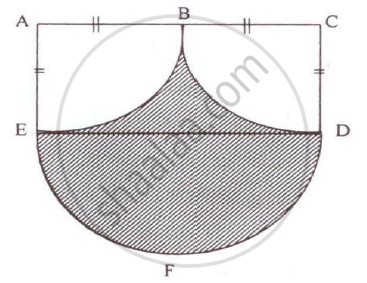
Calculate the area of the shaded region, if the diameter of the semicircle is equal to 14 cm. Take `pi = 22/7`

उत्तर
The diameter of the semi-circle is 14 cm.
ED = AC = 14 cm
Therefore, AB = BC = AE = CD = 7 cm
Area of the shaded region = Area of semi-circle EFD [Area of rectangle AEDC – 2 quarter circle]
`= 1/2 pir^2 + [AE xx ED - 2 xx 1/4 pir^2]`
`= 1/2 pir^2 + AE xx AE - 1/2 pir^2`
= 7 x 14
`= 98 cm^2`
APPEARS IN
संबंधित प्रश्न
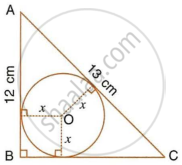
ABC is a right angles triangle with AB = 12 cm and AC = 13 cm. A circle, with centre O, has been inscribed inside the triangle.
Calculate the value of x, the radius of the inscribed circle.
Prove that the parallelogram, inscribed in a circle, is a rectangle.
Prove that the rhombus, inscribed in a circle, is a square.
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.
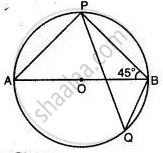
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
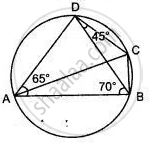
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.
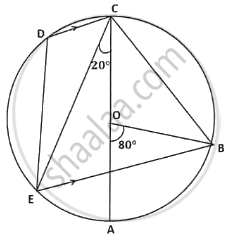
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED