Advertisements
Advertisements
प्रश्न
Two chords AB and CD intersect at P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD at the centre O is equal to twice the angle APC.
उत्तर
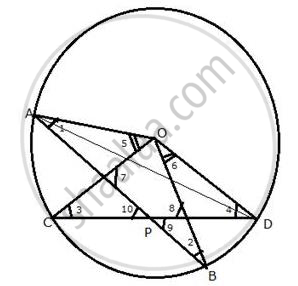
Given: Two chords AB and CD intersect each other at P inside the circle. OA, OB, OC and OD are joined.
To prove: ∠AOC + ∠BOD = 2∠APC
Construction: Join AD.
Proof: Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle.
∠AOC = 2∠ADC ...(1)
Similarly,
∠BOD = 2∠BAD ...(2)
Adding (1) and (2),
∠AOC + ∠BOD = 2∠ADC + 2∠BAD
= 2(∠ADC + ∠BAD) ...(3)
But ΔPAD,
Ext. ∠APC = ∠PAD + ∠ADC
= ∠BAD + ∠ADC ...(4)
From (3) and (4),
∠AOC + ∠BOD = 2∠APC
APPEARS IN
संबंधित प्रश्न
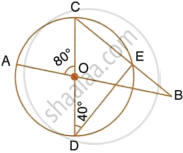
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in:
- ∠DCE,
- ∠ABC.
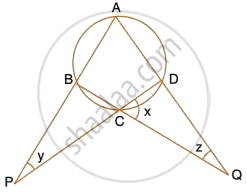
Calculate the angles x, y and z if :
`x/3 = y/4 = z/5`
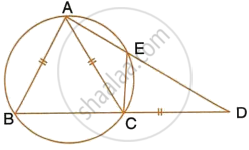
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate :
- Angle ABC
- Angle BEC
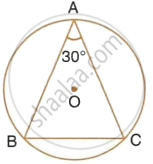
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.
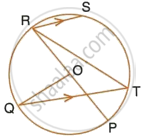
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
- angle QTR
- angle QRP
- angle QRS
- angle STR
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
(iii) angle QRS
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
(iv) angle STR

In the given figure, O is the center of the circle and the length of arc AB is twice the length of arc BC. If ∠AOB = 100°,
find: (i) ∠BOC (ii) ∠OAC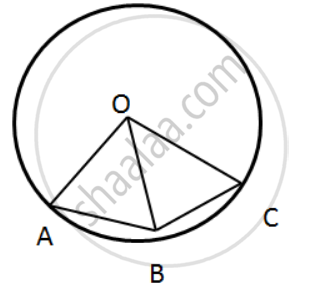
In the given figure, AB is a side of a regular hexagon and AC is a side of a regular eight-sided polygon.
Find:
(i) ∠AOB
(ii) ∠AOC
(iii) ∠BOC
(iv) ∠OBC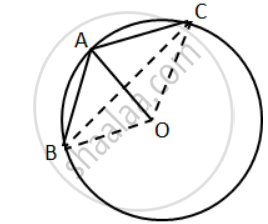
In the given figure, the lengths of arcs AB and BC are in the ratio 3:2. If ∠AOB = 96°, find:
- ∠BOC
- ∠ABC