Advertisements
Advertisements
प्रश्न
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
उत्तर १
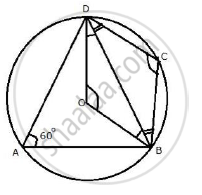
∠ BOD = 2 ∠BAD = 2 × 60° = 120°
And ∠ BCD = `1/2` Refelx (∠BOD) ( 360° - 120°) = 120°
(Angle at the centre is double the angle at the circumference subtended by the same chord
∴ ∠CBD + ∠CDB =180° - 120° = 60°
(By angle sum property of triangle CBD)
Again, ∠OBD+ ∠ODB=180° - 120° = 60°
(By angle sum property of triangle OBD)
∴ ∠OBD + ∠ODB = ∠CBD+ ∠CDB
उत्तर २
Here, ∠ BOD = 2 ∠BAD = 2 × 60° = 120°.
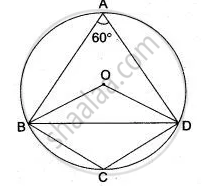
Now in Δ BOD,
∠OBD + ∠ODB = 180° - 120° = 60° ....(i)
Also, ∠DAB + ∠DCB = 180° ...(ABCD is cyclic quadrilateral)
∠DCB = 180° - 60° = 120° ...(ii)
∴ In Δ BCD,
∠ CBD + ∠CDB = 180° - ∠DCB = 180° - 120° = 60°
from (i) and (ii), we get the required result.
∴ ∠OBD + ∠ODB = ∠CBD+ ∠CDB.
Hence proved.
APPEARS IN
संबंधित प्रश्न
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

Use the given figure to find:
- ∠BAD,
- ∠DQB.
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
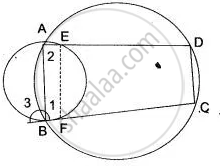
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
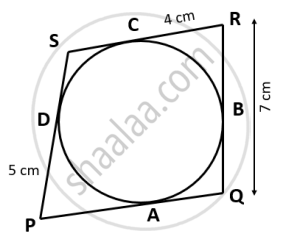
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: