Advertisements
Advertisements
प्रश्न
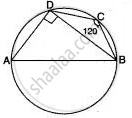
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA
उत्तर
(i) Since AOB is a diameter
∴ ∠ADB = 90° ...( C is a semi-circle)
Also, ABCD is a cyclic quadrilateral.
∴ ∠BCD + ∠BAD = 180°
∠BAD = 180° - 120°
⇒ ∠BAD = 60°
(ii) Now, In Δ BAD,
∠BAD + ∠BDA + ∠DBA = 180°
60° + 90° + ∠DBA = 180°
∠DBA = 180° - 150°
∠DBA = 30°
APPEARS IN
संबंधित प्रश्न
In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
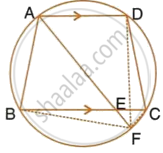
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
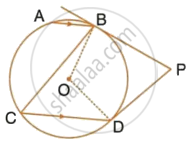
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
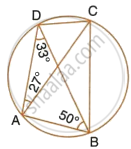
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
In the following figure, Prove that AD is parallel to FE.

Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
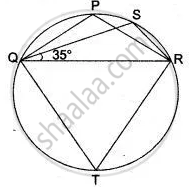
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.